 Identification
Identification
|
| Official Latin term | relatio SetIn |
| Official subsidiary term | SetIn relation |
| Unit identifier | TAH:U19555 |
| Unit type | single |
| Materiality | non physical entity |
 Navigation
Navigation
|
 Taxonomic definition
Taxonomic definition
|
| Taxonomic definition | The SetIn relation is a relation of set of immaterial partition of immaterial entity [relatio classis partitionis incorporeae rei incorporeae] which specifies an immaterial set from an immaterial singular entity. |
 Documentation
Documentation
|
|
The SetIn relation. The SetIn relation is a specialisation of the PartOf relation and contributes as such to the definition of the partonomic hierarchy of TAH.The SetIn relation is a link between a father immaterial singular unpaired entity and a child immaterial composite unpaired entity. The father entity necessarily has a dimension equal to the dimension of its child. In other words, through this relation a set of spaces is a part of a space.Example: [classis cisternarum subarachnoidearum cranialium] -> (SetIn) -> [spatium subarachnoideum ].Name: SetInDisplay name: is set inInverse relation name: HasSetInAcronym: STIConceptual schema: [Child entity A] -> (SetIn) -> [Father entity B]Child entity A: immaterial composite unpairedFather entity B: immaterial singular unpaired. |
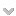 Partonomy
Partonomy
|
| TAH:U19555 |
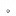 relatio SetIn relatio SetIn
|
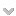 Taxonomy
Taxonomy
|
| FMA:62955 | |
| FMA:67115 | |
| FMA:45723 | |
| FMA:50627 | |
| FMA:67530 | |
| TAH11386 | |
| TAH13708 | |
| TAH13710 | |
| TAH:G19555 |
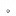 relatio SetIn relatio SetIn
|
| Date: 26.03.2022 |

